EDICT

„În prezent, orice şcolar calculează lungimea unei circumferinţe după diametrul ei, într-un mod mai exact decât cel mai înţelept preot din străvechea ţară a piramidelor sau cel mai iscusit arhitect al măreţei Rome“[1]… fără să bănuiască, însă, că în calculele lor se strecoară un număr care a adus multă nelinişte în rândul celor mai mari matematicieni ai lumii de-a lungul mileniilor.

Numărul π este o constantă matematică ce reprezintă raportul algebric dintre circumferinţa şi diametrul oricărui cerc din spaţiul euclidian.

La propunerea  matematicianului galez William Jones în 1706, susţinută şi popularizată apoi de Leonhard Euler în 1737, această constantă primeşte, în notaţia sa, simbolul π („pi“ în citire, corespunde literei p în scrierea română/ latină) reprezentând prima literă a cuvântului grecesc περίμετρος (perimetros = perimetru) sau περιφέρεια (perifereia = periferie).

În ce priveşte valoarea acestui număr, aceasta cunoaşte o istorie foarte îndepărtată şi plină de peripeţii.

„A fǎcut marea turnatǎ din aramǎ. Avea zece coţi de la o margine pânǎ la cealaltǎ, era rotundǎ de tot, înaltǎ de cinci coţi, şi de jur împrejur se putea mǎsura cu un fir de treizeci de coţi.“ (1Regi 7:23; 2 Cronici 4:2)

Acest text din Biblie, în care observăm valoarea trei pentru numărul π, ne certifică faptul că, în diferite forme, valori sau notaţii, acest număr era deja prezent în viaţa oamenilor cu foarte mult timp în urmă.

Şi vechii evrei utilizau aceeaşi valoare 3 pentru numărul π, însă babilonienii, mai exacţi, foloseau în calcule

Egiptenii antici cunosc o aproximare mai bună, astfel, pe papirusul Rhind [2]  (vezi figura 1), calculând aria unui disc, scribul Almes a utilizat

Figura 1: O porţiune din papirusul Rhind [3]

În geometria sacrală indiană, în aşa-numitele sulba-sutre care provin din secolele al VIII-lea – al III-lea î.Hr., apar valori remarcabile pentru π: Āryabhata (499 d.Hr.) calculează perimetrul poligonului înscris cu 386 de laturi şi obţine valoarea

Folosind poligoane regulate cu 96 de laturi, Arhimede a estimat valoarea lui π ca fiind 

Şi în China antică au existat preocupări cu privire la valoarea lui π. Astfel,  urmând calea lui Arhimede, Liu-Hui (236 d.Hr.), ajunge la poligonul cu 192 de laturi şi găseşte π = 3,14 iar Tsu Ch’ing-Chi (462 d.Hr.), avea să dea o valoare surprinzător de precisă pentru acele vremuri, şi anume:  3,1415926 < π < 3,1415927, iar pentru scopuri practice ia π = 355/113  sau π = 22/7.

Fr.Viète, utilizând tot metoda lui Arhimede, ajungând până la poligoanele înscrise şi circumscrise cu 6*2^16  laturi, a determinat valoarea lui π cu 9 zecimale exacte.

Cele mai bune aproximări pe această cale provin de la câţiva matematicieni olandezi dintre care îl amintim pe Ludolph van Ceulen care, în 1596, a găsit pentru π 20 de zecimale exacte cu ajutorul poligonului cu 15*2^37 laturi, cu ajutorul formulei , iar mai târziu, printr-o muncă laborioasă, a obţinut 35 de zecimale exacte calculând perimetrul poligonului cu 2^62 laturi şi a lăsat prin testament ca acest număr să fie gravat pe mormântul său funerar.

Între anii 1946 şi 1947 D.F. Ferguson (Universitatea din Manchester) şi, independent de el, J.W. Wrench (din Washington) au calculat valoarea lui π cu 808 zecimale şi s-au simţit satisfăcuţi descoperind că în calculele lui Shenks (care în anul 1873 a publicat o valoare a lui π cu 707 zecimale) au descoperit o eroare începând cu cifra a 528-a.

Mai târziu, în 1949, cu ajutorul unei maşini electronice de calcul a Universităţii Pensilvania de tip ENIAC, s-a calculat valoarea lui π cu 2040 de zecimale (în timp de 96 de ore).

O preocupare constantă a matematicienilor a fost ameliorarea prin diferite metode a aproximaţiei numărului π.

Astfel, istoria matematicii consemnează formule de calcul ale lui π cu care se poate obţine aproximaţia dorită:

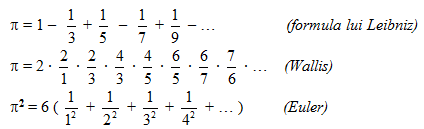
Tot Euler a descoperit relaţia dintre funcţia exponenţială şi funcţiile circulare: 

Punând în această egalitate x = π, obţinem e^iπ = -1 (sau e^iπ + 1 = 0, dacă am vrea, pentru frumuseţea matematicii, să scoatem mai multe elemente primordiale în evidenţă) relaţie care va duce la descoperirea naturii numărului π.

Despre caracterul său iraţional găsim referiri încă de prin secolul IX în scrierile lui Abu Abdullah Muhammad bin Musa al-Khwarizmi [4] apoi prin sec XII când Maimonides [5] spune că este sigur de iraționalitatea lui π dar o demonstrația completă a fost realizată abia în 1768 de către Johann Heinrich Lambert [6].

Mai târziu, în anul 1882, matematicianul german Ferdinand Lindemann [7] stabileşte caracterul transcendent al numărului π, punând capăt frământărilor milenare a matematicienilor şi, cu această ocazie, tranşând definitiv problema cvadraturii cercului. Acest fapt nu a oprit pe mulţi matematicieni să-i găsească şi alte zecimale.

În anul 2013, doi cercetători japonezi, cu ajutorul unui super calculator, au reușit să treacă de bariera de calcul a 10000 de miliarde de zecimale pentru numărul π şi calculul continuă.

Astfel de eforturi pentru astfel de calcule sau aproximări nu au nici valoare teoretică şi, cu atât mai puţin, valoare practică în condiţiile în care din 1882 deja s-a tranşant natura acestui număr.

Pentru a calcula, spre exemplu, lungimea ecuatorului cu o precizie de până la 1cm, ar fi suficient primele nouă zecimale ale numărului π.

Matematicianul Grave[8]  a demonstrat într-un mod extrem de clar absoluta inutilitate chiar şi a primei sute de cifre zecimale din valoarea lui π. El a spus că, dacă ne-am imagina o sferă, a cărei rază să fie egală cu distanţa de la Pământ la steaua Sirius (132*10^10  km), am umple această sferă cu bacterii, presupunând că în fiecare milimetru cub al sferei ar exista câte un bilion (10^10) de bacterii, apoi toate aceste bacterii le-am aşeza într-o linie dreaptă în aşa fel ca distanţa dintre două bacterii învecinate să fie egală din nou cu distanţa de la Pământ la steaua Sirius, atunci acceptând acest segment fantastic drept diametru al unui cerc, am putea calcula lungimea sa cu o precizie microscopică, adică de până la 1/1000000  mm, folosind 100 de zecimale după virgulă din valoare lui π [9].

Pentru calculele obişnuite cu π este pe deplin suficient să ţinem minte primele două zecimale (3,14), iar pentru calcule mai exacte e suficient să reţinem expresia:

„Aşa e uşor a scrie renumitul şi utilul număr din carte“ [10],

în care zecimalele numărului π sunt egale cu numărul de litere ale fiecărui cuvânt.

Şi în privinţă construcţiei numărului π au fost depuse eforturi importante de-a lungul timpului ce au avut ca rezultat idei şi tehnici de construcţii mai mult sau mai puţin interesante sau cu o mai mare sau mai mică aproximare.

Să prezentăm o metodă de construcţie a numărului π cu o aproximaţie destul de bună (vezi figura 2).

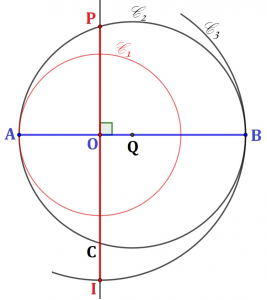
Figura 2

Construcţia:

Demonstraţia:

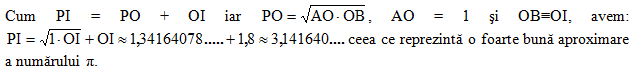
Referințe:

[1] I.I. Perelman, Geometria distractivă, Ed. Ştiinţifică, Bucureşti, 1965, pagina 200.

[2] Papirusul Rhind este un document din Egiptul antic datat în jurul anului 1650 î.Hr. și care conține 85 de probleme de matematică. Poartă numele egiptologului Alexander Henry Rhind, care l-a achiziționat în anul 1858 din Luxor. Se crede că este copia unuia mai vechi, datând din perioada 1842-1800 î.Hr. Este lung de aproape 20 m și lat de 32 cm și se păstrează la British Museum. Papirusul a fost scris de scribul Ahmes și poartă titlul: Instrucțiuni pentru a cunoaște toate lucrurile secrete (conform https://ro.wikipedia.org/wiki/Papirusul_Rhind)

[3] Apud https://ro.wikipedia.org/wiki/Papirusul_Rhind

[4] Abu Abdullah Muhammad bin Musa al-Khwarizmi (aprox. 780 – 845) savant, astronom/astrolog, matematician și scriitor persan;

[5] Moise Maimonide (n. 30 martie 1135, Córdoba – d. 13 decembrie 1204, Fustat, azi Cairo) a fost un filosof, medic și teolog evreu din Evul Mediu.

[6] Johann Heinrich Lambert (n. 26 august 1728 – d. 25 septembrie 1777) a fost un matematician, fizician și astronom elvețian;

[7] Carl Louis Ferdinand von Lindemann (12 aprilie 1852 – 6 martie 1939) matematician german.

[8] Dmitri Aleksandrovici Grave (1863-1939) matematician rus de etnie ucraineană;

[9] I.I. Perelman, Geometria distractivă, Ed. Ştiinţifică, Bucureşti, 1965, pagina 202;

[10] idem

Bibliografie:

1. Perelman, I.I. (1965). Geometria distractivă. București: Editura Științifică.
2. Păduraru, Vasile (2018). Construcţii geometrice cu rigla şi compasul – abordări metodice. Iași: Editura Ştef.
3. ro.wikipedia.org/wiki/Papirusul_Rhind