”Nowadays, any student calculates the length of a circumference after its diameter, in a more precise way than any priest in the ancient country of the pyramids, or the most skilled architect of the great Rome could have ever done“… without suspecting though, that in their calculations there is a number that interferes, a number which has concerned even the greatest mathematicians over the years.
This number π is a mathematical constant that represents the algebraic report between the circumference and the diameter of any circle in the Euclidian space.
On the Walsh mathematician William Jones’s proposal in 1706, supported and promoted later by Leonhard Euler in 1737, this constant gets as its representation the symbol π („pi“ in reading corresponds to the letter „p“ in the Roman/ Latin writing), meaning the first letter of the Greek word περίμετρος (perimetros = perimeter), or περιφέρεια (perifereia = periphery).
Regarding the value of this number, it has a very faraway and full of adventures history.
”He made the big turntable of brass. It had ten cubits from one side to the other, it was totally round, tall of five cubits and all around it could be measured with a thread of thirty cubits“. (1 Kings7:23; Chronics 4:2)
This text from the Bible, in which we notice the value 3 for number π, ensures the fact that, in different shapes, values or representations, this number was already present in people’s life long time ago. Even the ancient Hebrew people were using the same value 3 for number π, but the Babylonians, being more accurate, were using in calculations
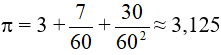
The ancient Egyptians knew a better approximation, thus, on Rhind papyrus (see figure 1), calculating the area of a discus, scribe Almes used
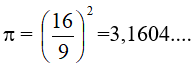

In the sacred Indian geometry, in the so called sulba-sutras that come from the 8th –3rd BC centuries, remarkable values for π appear: Āryabhata (499 BC.) calculated the perimeter of the inscribed polygon with 386 sides and he got the value π = 3,1416.
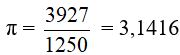
Using regular polygons with 96 sides, Archimedes estimated the value of π as being
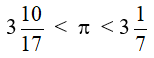
Even in the ancient China there were preocupations regarding the value of π. So, following Archimedes’s method, Liu-Hui (236 B.C.) gets to the polygon with 192 sides and he calculates π = 3,14 and Tsu Ch’ing-Chi (462 B.C.) was the one who gave it a surprisingly precise value for those times, meaning: 3,1415926 < π < 3,1415927, and for practical purposes, he took
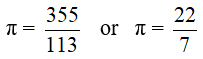
Fr.Viète, using also Archimedes’s strategy, getting to the inscribed and circumscribed polygons with 6∙216 sides, determined the value for π with 9 precise decimals.
The best approximations obtained this way come from a few Dutch mathematicians, like Ludolph van Ceulen, who in 1596 found for π 20 precise decimals with the help of the polygon with 15∙237 sides, using the formula
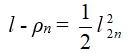
and later, through a laborious work, he got 35 precise decimals calculating the perimeter of the polygon with 262 sides and he asked in his will this number to be graven on his funeral stone.
Between 1946 and 1947, D.F. Ferguson (Manchester University) and, independent from him, J.W. Wrench (in Washington) calculated the value of π with 808 decimals and felt satisfied discovering that in Shenks’s calculations (who in 1873 published a value for π with 707 decimals) there was an error beginning with the 528th figure.
Later, in 1949, with the help of an electronic computing machine belonging to Pennsylvania University, ENIAC type, the value of π with 2040 decimals was calculated (during 96 hours).
A constant preoccupation of mathematicians represented the improvement through different methods of the approximation of number π.
Thus, the history of mathematics records calculating formula for π, with the help of which the desired approximation can be obtained:
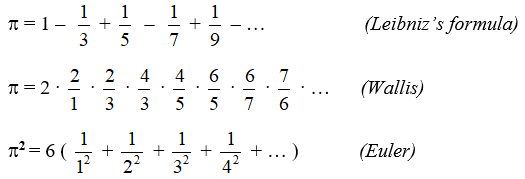
Also, Euler discovered the relation between the exponential function and the circular functions: eix = cos x + i sin x.
Considering in this equality x = π, we get eiπ = -1 (or eiπ + 1 = 0, if we wanted, for the sake of mathematics, to highlight more primordial elements), a relation which would lead to the discovery of the nature of number π.
About its irrational character, we find references since the IXth century in Abu Abdullah Muhammad bin Musa al-Khwarizm’s writings, then, in the XIIth century, when Maimonides said that he was sure about the irrationality of π, but a fully demonstration was performed only in 1768 by Johann Heinrich Lambert.
Later, in 1882, the German mathematician Ferdinand Lindemann establishes the transcendental character of π, ending up, this way, to the mathematicians’ millenary kneadings and on this occasion, they also cut permanently the quadrature of the circle problem. This fact didn’t stop many other mathematicians finding it some other decimals.
In 2013, two Japanese researchers, with the help of a super computer, managed to pass over the barrier of calculating with 10,000 billiard decimals for the same number π and the calculation goes on.
Such efforts for such calculations or approximations have no theoretical value and even less, a practical value, given that since 1882 the nature of this number has already been established.
For measuring, for example, the length of the Equator, with a precision of up to 1 cm, it would be enough to know the first 9 decimals of number π.
Dimitri Grave, a Mathematics teacher, proved in an extremely clear manner the absolute uselessness even of the first hundred decimals from the value of π. He said that if we imagined a sphere, whose radius was equal with the distance from Earth to star Sirius (132·1010 km), we would fill this sphere with bacteria, assuming that in each cubic millimeter would exist one billion (1010) bacteria, then we would arrange all these bacteria in a straight line so that the distance between two neighbour bacteria is equal again with the distince between Earth and Sirius, then accepting this fantastic segment as the diameter of a circle, we would be able to calculate its length with a microscopic precision, meaning up to 1/1000000, using one hundred decimals after the comma from the value of π.
For common calculations with π it is fully enough to remember the first two decimals (3, 14) and for more precise calculations it is enough to retain the Romanian expression „Aşa e uşor a scrie renumitul şi utilul număr din carte“ (This is the easy way to write the well-known and the useful number in the book), or ”How I need a drink, alcoholic of course, after the heavy lectures involving quantum mechanics”, in which the decimals of the number π are equal with the number of letters of each word.
Also, regarding the construction of number π researchers have made important efforts over the time, which had as a result ideas and construction techniques more or less interesting, or with a higher or lower approximation.
Let’s introduce a method of construction of number π with a quite good approximation (see Figure 2):
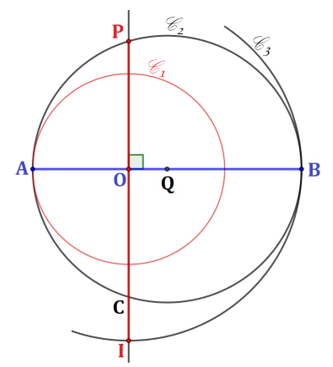
Method of construction:
Demonstration:
Bibliography
1. Perelman, I.I. Geometria distractivă, Editura Științifică, București, 1965;
2. Vasile Păduraru Construcţii geometrice cu rigla şi compasul – abordări metodice,
Editură Ştef, Iaşi, 2018.
3. ro.wikipedia.org/wiki/Papirusul_Rhind
* * *
Written by Vasile Păduraru, Mathematics teacher,
Mărgineni School, Neamţ County, Romania
Translated by Nicoleta Orza, English teacher,
Dumbrava Roşie School, Neamţ County, Romania

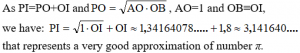
Trebuie să fii autentificat pentru a publica un comentariu.