EDICT

Lucrarea „Numere complexe în electrotehnică” este reprezentativă pentru a evidenția corelarea interdisciplinară în predarea matematicii. Prezentarea noțiunilor despre numere complexe, dar și aplicarea acestora în electrotehnică se dorește a fi un exemplu de bună practică. Aceasta interdependență între matematică și disciplinele tehnice este posibilă deoarece limbajul matematic este universal, internațional, ceea ce ajută la circulația și acumularea ordonată a rezultatelor matematice prin efortul comun al tuturor generațiilor. Considerăm că acest mod de abordare este eficient atât pentru cadrele didactice, cât și pentru elevi.

Prezentarea noțiunilor despre numere complexe

1) Mulţimea numerelor complexe

a este partea reală a numărului complex z; a = Re(z)

bi este partea imaginară a numărului complex z; b este coeficientul părții imaginare, b = Im(z)

i² = -1 este unitatea imaginară

este mulţimea numerelor complexe pur imaginare

este forma algebrică a numărului complex z

2) Egalitatea a două numere complexe: dacă z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, a_1, b_1, a_2, b₂ Î R, i² = -1, atunci:

3) Adunarea şi înmulţirea a două numere complexe scrise sub formă algebrică:

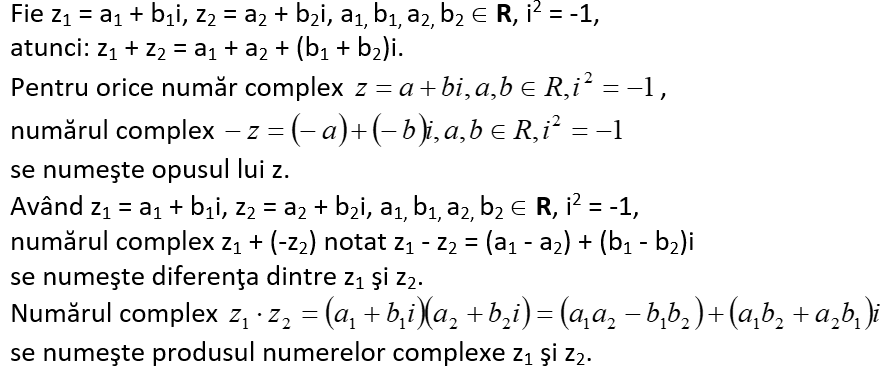
4) Conjugatul unui număr complex:

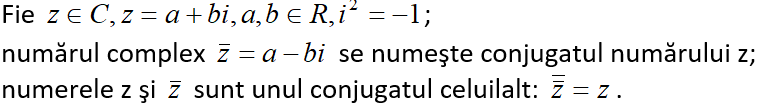
5) Modulul unui număr complex: fie ; se numeşte modulul lui z, notat , numărul real pozitiv: .

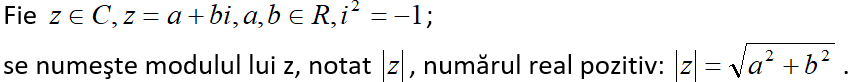
Aplicarea numerelor complexe în electrotehnică

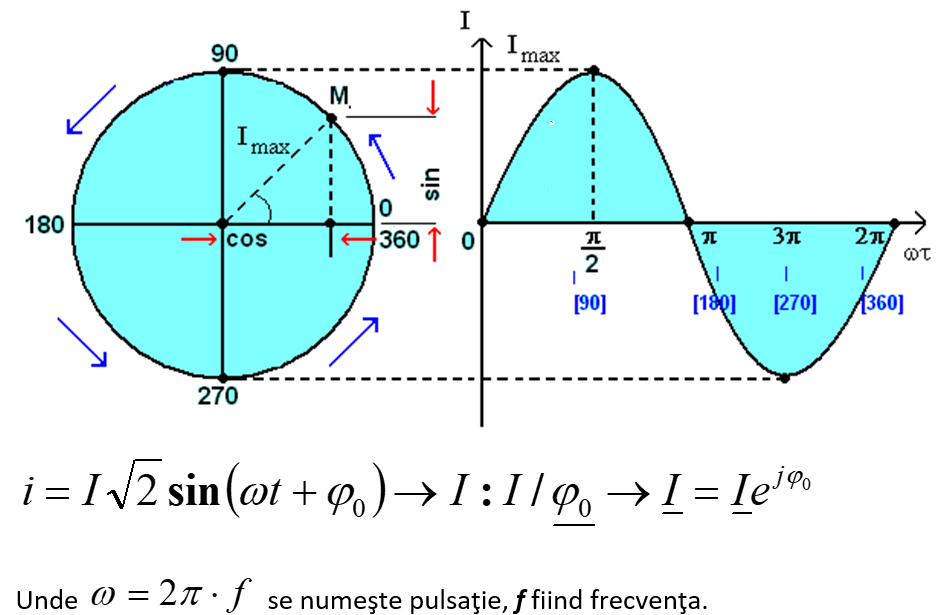
Reprezentarea în complex a mărimilor sinusoidale

1.     În reprezentarea vectorială se foloseşte proprietatea funcţiilor sinusoidale de a putea  fi puse în corespondenţă cu vectori liberi din plan.

2.     Oricărui număr complex îi corespunde în mod biunivoc un punct în planul complex şi deci, îi corespunde şi vectorul de poziţie al acestuia faţă de originea planului.

Identificând planul vectorilor liberi cu planul complex, putem stabili o corespondenţă biunivocă între mulţimea funcţiilor sinusoidale de timp şi mulţimea numerelor complexe, rezultă deci, reprezentarea analitică a funcţiilor sinusoidale, denumită repezentare în complex.

Impedanţa. Calculul impedanţelor echivalente

Impedanţa este o mărime care caracterizează funcţionarea elementelor de circuit în curent alternativ.

Legea lui Ohm în c.a.: Z = U/I

Impedanţele se pot reprezenta prin

a)     diagrame fazoriale

b)     numere complexe

Impedanţa complexă a circuitului :

Obs. S-a notat  unitatea imaginară

pentru a evita confuzii cu simbolul i utilizat in electrotehnică pentru valoarea instantanee a curentului alternativ.

Circuit R-L-C serie

Gruparea unor elemente rezistive, inductive şi capacitive încât curentul electric să fie unic şi cu aceeaşi valoare, constituie circuitul R-L-C serie de curent alternativ.

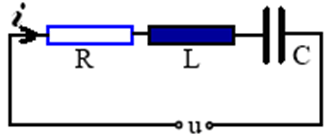
La bornele fiecărui element de circuit se va regăsi câte o tensiune corespunzătoare, conform legii lui Ohm:

U_R = RI, U_L = X_LI, U_C = X_CI, unde X_L = Lω, X_C = 1/Cω

Impedanța este o mărime globală.

Pentru calculul impedanţei echivalente, reactanţele circuitului pot fi sumate numai vectorial, sau ca numere complexe, deoarece:

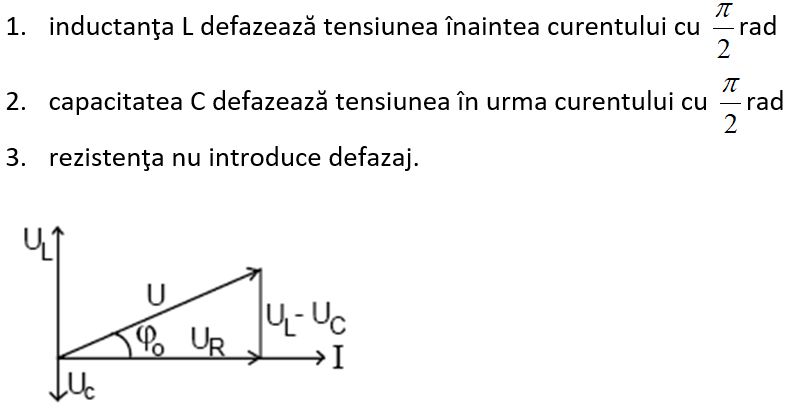
Impărţind diagrama tensiunilor la I, rezultă diagrama impedanţelor:

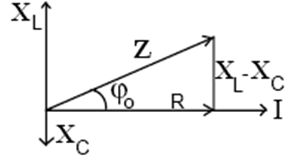
Identificând planul vectorilor liberi cu planul complex, rezultă:

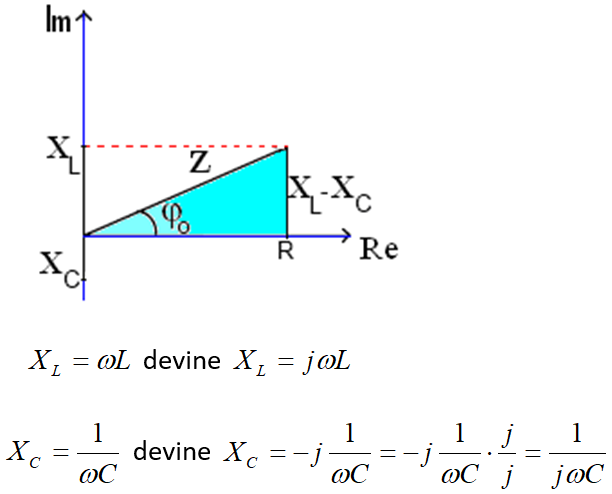
Ținând seama de aceste observații, se poate scrie

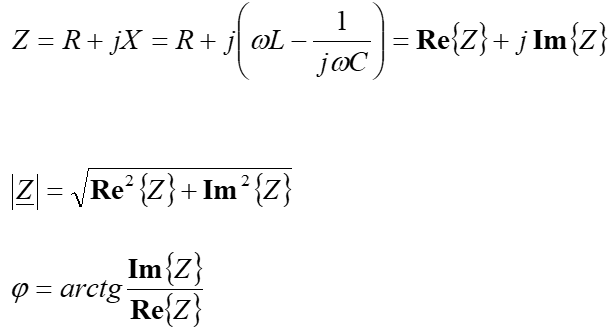
Din reprezentarea fazorială a celor trei tensiuni, defazate corespunzător fiecărui element de circuit, rezultă că există o defazare  dintre tensiunea aplicată U şi intensitatea I a curentului electric.

Aplicații:

• Să se determine x,y ∈ R, care verifică egalitatea: (x + iy)² = 7 + 5i.
• Fie z = 1 + 2i, z’ = 2 + i. Calculaţi: z + z’; z’ + z; -z; z – z’; z’ – z; z z’; z’z.
• Pentru z = -3 + 4i,

• Determinaţi modulul numărului complex z = 9 – 12i.
• Aplicatie in electrotehnica:

Să se determine impedanţa complexă echivalentă a circuitului RLC paralel:

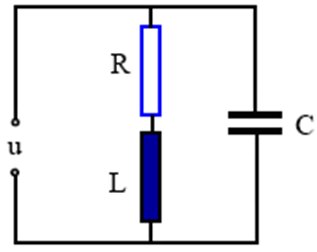
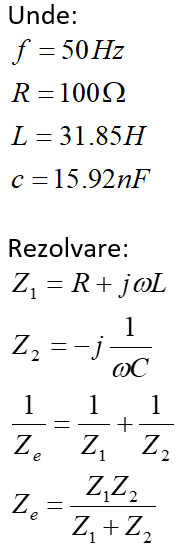
Se poate lucra literal astfel:

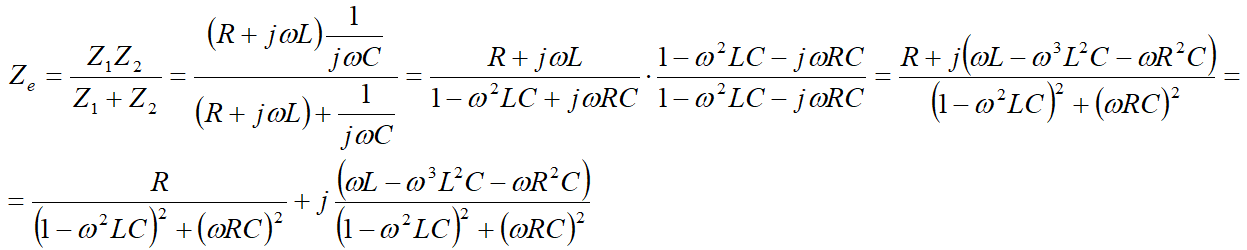
Sau se pot folosi valorile numerice astfel:

ω=2πf

R=10⁵Ω

L=31,85H

C=15,92*10^-9F

Z₁=R+j Ωl=10⁵+j*314*31,85=10⁵+10⁴j

Bibliografie
Manualul de matematică, clasa a X-a, editura Mathpress, autor Mircea Ganga
Manual de electrotehnica, clasa a X-a, autori: Gheorghe Frăţiloiu, Andrei Ţuglea, Mihai Vasiliu, Maria Catană
Curs universitar „Didactica Matematicii”
Curs „Competenţe cheie TIC în curriculumul şcolar”

* * *

Autoare:
Profesor Rodica Ciucă, Colegiul Economic „Ion Ghica” Brăila
Inginer Michaela Grădinaru, Liceul Tehnologic „Anghel Saligny”, Brăila