În contextul didacticii matematicii, dezvoltarea progresivă a competențelor de rezolvare a problemelor constituie un obiectiv fundamental al procesului educațional, marcând tranziția de la gândirea concretă la cea abstractă. Această evoluție metodologică reflectă principiile constructivismului pedagogic, potrivit căruia elevii își construiesc cunoștințele prin trecerea graduală de la strategii intuitive la sisteme formale de reprezentare și manipulare simbolică. Comparația între metodele aritmetice și cele algebrice de rezolvare a problemelor evidențiază această progresie cognitivă naturală, oferind cadrului didactic oportunitatea de a proiecta secvențe de învățare care respectă ritmul de dezvoltare intelectuală al elevilor, facilitând astfel o înțelegere mai profundă a conceptelor matematice și dezvoltarea unei gândiri matematice flexibile și riguroase.
Două dintre cele mai comune moduri de rezolvare a unei probleme sunt utilizarea metodelor aritmetice și metoda algebrică. Rezolvarea ecuațiilor este o abilitate esențială în matematică, reprezentând un mijloc fundamental prin care se pot exprima și soluționa probleme din viața reală sau din științe exacte. Fiecare dintre acestea are propriile sale avantaje și limite, fiind potrivite în contexte diferite.
Metodele aritmetice se bazează pe raționamente logice, pași concreți și calcule numerice simple, fiind adesea utilizată în clasele primare sau în probleme unde se poate deduce intuitiv răspunsul. În schimb, metoda algebrică implică utilizarea simbolurilor și a operațiilor algebrice pentru a transforma și rezolva ecuații sau sisteme de ecuații, fiind mai generală, mai riguroasă și aplicabilă într-un spectru mai larg de situații, în special în clasele gimnaziale și liceale.
Această comparație dintre cele două metode evidențiază modul în care gândirea matematică evoluează de la forme intuitive la structuri abstracte și generalizabile, pregătind elevii pentru concepte mai avansate.
Conform programei de matematică, studiul ecuațiilor începe abia în clasa a VI-a, cu ecuațiile în mulțimea numerelor întregi. În ciclul primar, precum și în clasa a V-a, elevii rezolvă probleme folosind doar metode aritmetice. Acestea sunt mai ușor de înțeles pentru copiii de vârste mici. Tot în clasa a VI-a, se introduce rezolvarea problemelor cu ajutorul ecuațiilor.
Voi prezenta în continuare două probleme de matematică rezolvate prin o metodă aritmetică și prin metoda algebrică.
1. În curtea unui fermier sunt găini și oi, în total 26 capete și 80 picioare. Aflați câte găini și câte oi sunt la fermă.
I. Rezolvare aritmetică, utilizând metoda falsei ipoteze:
Presupunem că la fermă sunt doar găini.
Calculăm numărul de picioare: 26 · 2 = 52 picioare.
Dar trebuie să fie 80 de picioare, deci facem diferența 80 – 52 = 28 picioare (ar mai trebui).
Această diferență apare din diferența numărului de picioare: 4 – 2 = 2.
Efectuăm împărțirea 28 : 2 = 14, deci sunt 14 oi.
Numărul total de animale fiind 26, 26 – 14 = 12 găini.
Răspuns: sunt 12 găini și 14 oi.
II. Rezolvare algebrică:
Notăm necunoscutele: x – număr de găini, y – număr de oi
Scriem ecuațiile:
x + y = 26, deci x = 26 – y
2x + 4y = 80
Înlocuind pe x cu 26 – y, obținem:
2(26 – y) + 4y = 80
52 – 2y + 4y = 80
2y = 80 – 52
2y = 28
y = 28 : 2
y = 14, de unde x = 26 – 14, x = 12
Răspuns: sunt 12 găini și 14 oi.
2. Suma a două numere naturale este 60. Împărțind numărul mai mare la cel mai mic, se obțin câtul 3 și restul 8. Aflați numerele.
I. Rezolvare aritmetică, utilizând metoda grafică:
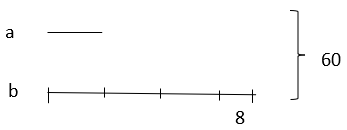
60 – 8 = 52 (4 segmente congruente)
52 : 4 = 13 (a)
b = 60 – 13 = 47
Răspuns: numerele sunt 13 și 47.
II. Rezolvare algebrică:
Notăm necunoscutele: a – numărul mai mic, b – numărul mai mare
Scriem ecuațiile:
a + b = 60
b = 3a + 8
Înlocuind pe b cu 3a + 8, obținem:
a + 3a + 8 = 60
4a = 60 – 8
4a = 52
a = 52 : 4
a = 13, de unde b = 60 – 13, a = 47
Răspuns: numerele sunt 13 și 47.
Alegerea metodei de rezolvare depinde de complexitatea problemei, de nivelul de abstractizare al elevului, dar și de obiectivele pedagogice urmărite. O abordare comparativă a celor două metode nu doar că oferă o înțelegere mai profundă a conceptelor matematice, dar contribuie și la formarea unei gândiri flexibile.
Rezolvarea problemelor matematice reprezintă una dintre cele mai eficiente metode de dezvoltare a gândirii logice și analitice.
Bibliografie
- Cuciureanu, D. (2002). Didactica matematicii. Editura Polirom.
- Ghiță, L., & Radu, C. (1998). Metodica predării matematicii în învățământul primar și gimnazial. Editura Didactică și Pedagogică.

Trebuie să fii autentificat pentru a publica un comentariu.