Poate geometria să devină din nou captivantă pentru elevi?

Predarea matematicii la nivel liceal, în special în clasa a IX-a, reprezintă un context favorabil pentru dezvoltarea gândirii logice, a spiritului de investigație și a creativității elevilor. Teorema cosinusului, cunoscută și sub denumirea de teorema lui Al-Kashi sau teorema generalizată a lui Pitagora, își are originile în mai multe civilizații antice. Deși ideea sa era utilizată încă din Antichitate de matematicieni greci precum Euclid și Hiparh, formularea explicită apare în secolul al XV-lea în lucrările matematicianului persan Ghiyath al-Din Jamshid al-Kashi.

Un avantaj major al teoremei cosinusului, în comparație cu teorema lui Pitagora, este aplicabilitatea sa universală: ea permite determinarea lungimilor laturilor sau a măsurilor unghiurilor în orice tip de triunghi, nu doar în cele dreptunghice.

Aplicații practice ale teoremei cosinusului:

• Topografie și cartografie – Teorema cosinusului este esențială pentru calculul distanțelor și pozițiilor pe hărți, fiind utilizată inclusiv în sistemele GPS și în studiul spațiilor neeuclidiene.
• Inginerie și construcții – Este folosită pentru determinarea unghiurilor și dimensiunilor elementelor structurale în proiecte complexe, precum poduri sau clădiri.
• Navigație – În navigația aeriană și maritimă, teorema ajută la stabilirea traseelor și a distanțelor dintre puncte aflate pe suprafața Pământului, considerat aproximativ
• Astronomie – Permite estimarea distanțelor dintre stele și alte corpuri cerești, fiind un instrument de bază în triangulația spațială.
• Grafică computațională – În animație și randare 3D, teorema cosinusului este utilizată pentru calculul iluminării și al reflexiilor, contribuind la obținerea unui realism vizual

Un exemplu atractiv care poate stârni interesul elevilor este „Problema comorii”, prezentată în cartea lui George Gamow „Unu, doi, trei… infinit”.

Indicații pentru căutător:

Pornește spre o anumită latitudine nordică și longitudine vestică, unde vei descoperi o insulă părăsită (coordonatele exacte au fost omise intenționat). Pe malul nordic al insulei se află o câmpie întinsă, în care se găsesc un singur stejar și un singur pin, precum și o veche spânzurătoare.

De la spânzurătoare, îndreaptă-te spre stejar, numărând pașii. Ajuns la acesta, întoarce-te la dreapta cu un unghi de 90° și parcurge același număr de pași, apoi fixează un țăruș. Revino la spânzurătoare, mergi spre pin, numărând din nou pașii. La pin, întoarce-te la stânga cu același unghi și parcurge din nou același număr de pași, înfigând un al doilea țăruș. Comoara se află la jumătatea distanței dintre cei doi țăruși.

Astfel de exemple arată cum geometria poate deveni nu doar utilă, ci și fascinantă, atunci când este legată de contexte concrete și povești captivante.

Stejarul, pinul şi spânzurătoarea dispar, se transformă în puncte. Întrucât nu ştim unde se află, punctul-spânzurătoare va fi notat cu M, punctul-stejar cu S punctul-pin cu P. Deci, din punctul de vedere al geometriei, problema va suna astfel: „Fie segmentul fix SP şi un punct variabil M într-un plan conţinând segmentul. Se construiesc SA ⊥ SM  astfel încât (SA) ≡ (SM ) şi MP ⊥ PB , (MP) ≡ (PB). Precizați poziția mijlocului segmentului (AB) faţă de (SP)”. Problema se poate rezolva exclusiv geometric folosind teorema cosinusurilor. Fie N mijlocul lui (𝐴𝐵).   Se calculează lungimea segmentului (PN ), (𝑆𝑁) cu teorema medianei în triunghiul ABP.

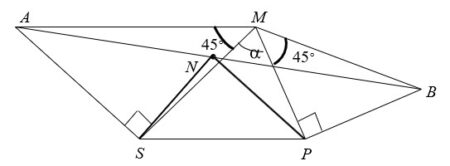
Deci, din relaţiile (6) şi (7) şi reciproca teoremei lui Pitagora, avem că ΔSPN este dreptunghic isoscel, m<(SNP) = 90^∘ , adică poziţia punctului N nu depinde de cea a lui M (locul unde se găsea spânzurătoarea)…

Teorema cosinusului este un instrument fundamental care permite rezolvarea triunghiurilor, facilitând o gamă largă de măsurători practice.

O altă perspectivă asupra predării

Teorema cosinusului, deși adesea percepută ca o simplă relație trigonometrică, are numeroase aplicații practice și atractive în domenii precum topografia, ingineria, navigația sau grafica digitală. Valorificarea acestor conexiuni permite transformarea unei lecții tradiționale de geometrie într-un veritabil laborator de explorare și aplicare a cunoștințelor.

1.  Etapa de predare – abordări inovative

a.  Povestea matematicii și explorarea interdisciplinară

Lecția poate debuta sub forma unei „călătorii istorice” interactive. Elevii, organizați în grupuri de cercetare, investighează contribuțiile diferitelor civilizații la dezvoltarea geometriei (greci, persani, arabi). Cu ajutorul unei hărți interactive afișate pe tabla digitală, sunt marcate zonele în care au activat Euclid, Hiparh și Al-Kashi, evidențiindu-se evoluția teoremei cosinusului. În acest mod, elevii realizează conexiuni culturale și științifice, învățând prin context și narațiune.

b.  Învățarea prin descoperire experimentală

Profesorul propune o situație practică: determinarea unei distanțe inaccesibile, cum ar fi distanța dintre două clădiri din curtea școlii. Elevii folosesc măsurători indirecte și aplică teorema cosinusului, utilizând instrumente moderne precum telemetrul, smartphone-ul sau aplicații de măsurare a unghiurilor. Activitatea stimulează gândirea critică și dezvoltă competențe practice.

c.  Modelare digitală

Prin utilizarea programelor de modelare 3D, precum GeoGebra, sau a aplicațiilor de realitate augmentată, elevii pot vizualiza triunghiuri în spațiu și pot observa modul în care modificarea unghiurilor sau a laturilor influențează rezultatele. Teorema cosinusului devine astfel intuitivă și ușor de înțeles, fiind explorată prin manipulare virtuală în timp real.

2.  Etapa de învățare activă – aplicații și jocuri didactice

„Problema comorii” – învățare prin joc și poveste matematică

Inspirată din lucrarea lui George Gamow, activitatea se desfășoară sub forma unei „vânători de comori geometrice”. Elevii, organizați în echipe, primesc o hartă a unei insule fictive, desenată pe tablă sau recreată în curtea școlii, și trebuie să determine poziția exactă a comorii folosind teorema cosinusului. Jocul dezvoltă cooperarea, capacitatea de aplicare a formulelor în contexte noi și gândirea logică.

Matematica în știință și artă

Se lansează provocarea „Descoperă teorema cosinusului în lumea reală!”. Fiecare elev alege un domeniu de interes (astronomie, arhitectură, navigație, grafică digitală) și realizează o prezentare, un poster sau o machetă care evidențiază aplicarea practică a teoremei. De exemplu, un elev pasionat de design 3D poate explica modul de calcul al direcției luminii într-un program de randare.

Atelier interdisciplinar de colaborare

În colaborare cu profesorii de fizică sau informatică, pot fi realizate proiecte STEAM, precum simularea mișcărilor planetelor sau a rotației Pământului. Aceste activități integrează relațiile trigonometrice în contexte științifice reale, consolidând învățarea interdisciplinară.

3.  Etapa de evaluare – metode creative și formative

Portofoliul digital

Elevii își reunesc activitățile într-un portofoliu digital (Google Sites, Canva, Padlet), care include măsurători, experimente, fotografii și prezentări. Evaluarea vizează corectitudinea aplicării teoremei, originalitatea, colaborarea și capacitatea de reflecție personală.

Autoevaluare și evaluare între colegi

După activitățile de grup, elevii completează chestionare de autoevaluare sau oferă feedback colegilor prin instrumente digitale precum Mentimeter, Kahoot sau Google Forms, consolidând procesul de învățare prin reflecție și feedback constructiv.

Evaluare prin provocări („Challenge Lab”)

Profesorul propune o situație practică nouă, de exemplu calcularea distanței dintre două puncte inaccesibile dintr-o imagine satelitară folosind Google Earth. Elevii aplică teorema cosinusului și își argumentează metoda, accentul fiind pus pe raționament, strategie și justificare.

Prin integrarea metodelor inovatoare – poveste istorică, învățare prin descoperire, instrumente digitale, jocuri matematice și evaluare creativă – teorema cosinusului depășește statutul de simplă formulă. Ea devine un instrument de înțelegere a realității, o provocare intelectuală și un mijloc prin care elevii învață să gândească matematic și interdisciplinar. Astfel, elevul de clasa a IX-a descoperă rolul esențial al matematicii în modelarea lumii înconjurătoare.