Un capitol aparte în matematica sfârșitului de ciclu primar și începutului ciclului gimnazial îl constituie problemele de mișcare (uniformă), în care se definește viteza (v) ca fiind raportul dintre deplasare (sau distanța parcursă d) și timpul (t) necesar mișcării: v=d/t.
Materialul prezintă, pe scurt, câteva tipuri de probleme de mișcare, după care oferă soluții ale unor probleme de aritmetică și nu numai, ce pot fi încadrate în alte categorii, pe baza exploatării relației unei așa – zise viteze.
Didactica matematicii caută constant metode inovatoare pentru a facilita înțelegerea conceptelor abstracte și pentru a dezvolta gândirea algoritmică a elevilor. Prezentul articol propune o abordare matematică aplicabilă în rezolvarea unor categorii variate de probleme. Extinderea conceptului de viteză dincolo de contextul cinematicii reprezintă un exemplu elocvent de generalizare matematică, ilustrând cum o formulă aparent specializată poate deveni un instrument euristic versatil. Această metodă didactică permite elevilor să identifice izomorfisme structurale între probleme aparent diferite și să aplice raționamente matematice similare în contexte diverse, dezvoltând astfel competențe esențiale precum abstractizarea, modelarea matematică și transferul algoritmic între domenii.
În cazul problemelor de cinematică (kineticos = mișcare, în limba greacă), se disting problemele de întâlnire dintre corpurile care se mișcă (mobile).
I.1. Probleme de întâlnire a mobilelor, când acestea se deplasează în același sens
În acest caz (vezi fig. 1), timpul de întâlnire (tI) al mobilelor poate fi dedus astfel:
AB + BI = AI ( 1 )
unde A = punctul de pornire al mobilului „1”, B = punctul de pornire al mobilului „2” şi I = punctul de întâlnire.

Fig. 1
Ţinând seama de relaţia dintre viteză, timp şi distanţă, relaţia (1) poate fi rescrisă astfel:
![]()
de unde:
![]()
Distanța parcursă de primul mobil până în momentul întâlnirii este:
![]()
I.2 Probleme de întâlnire a mobilelor, când acestea se deplasează în sens opus
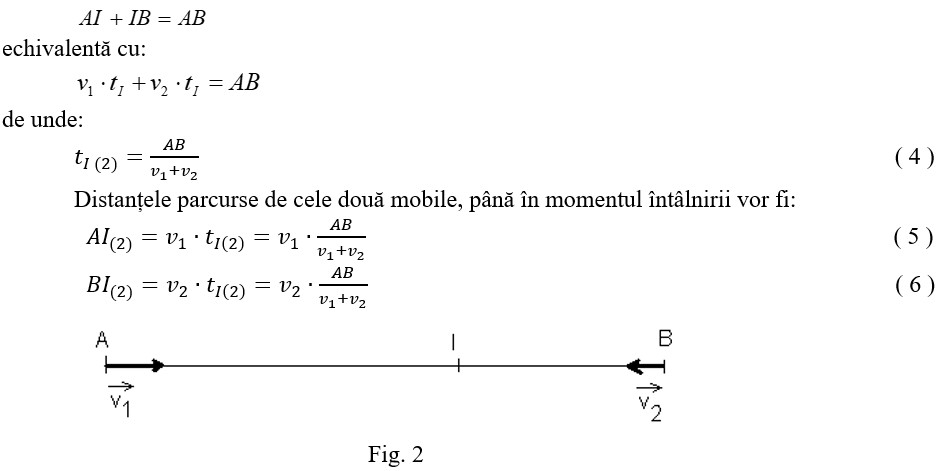
În acest caz, timpul de întâlnire (tI) al celor două mobile va fi dedus ( vezi fig. 2), din relaţia:
AI + IB = AB
echivalentă cu:
II. Probleme ce se pot rezolva extinzând noțiunea de viteză și abordând tehnici cinematice
Problema 1: Un angajat al unei edituri poate tehnoredacta un manuscris în 8 ore, iar un altul în 12 ore.
În cât timp ar termina de tehnoredactat manuscrisul, dacă ar lucra împreună?
Soluția 1 (Metoda reducerii la unitate):

Soluția 2 ( Metodă cinematică):

Următoarele probleme vor fi rezolvate doar apelând la noțiunea de viteză, fără a recurge la metodele clasice precum metoda reducerii la unitate sau regula de trei simplă.
Problema 2: Dacă rezolv câte 15 exerciții pe zi, în timpul vacanței, îmi rămân libere 3 zile, iar dacă rezolv câte 12 exerciții pe zi, atunci rămân nerezolvate 18 probleme.
Câte exerciții și câte zile de vacanță am?
Soluție:

Problema 3: Un bazin se poate umple prin două robinete în 12 ore. Primul robinet poate umple bazinul într-un timp cu 10 ore mai scurt decât timpul de umplere al celui de-al doilea.
În cât timp fiecare robinet, separat, poate umple bazinul?
Soluție:

Problema 4: Două echipe de muncitori lucrând împreună pot termina o lucrare în 12 ore. După ce au lucrat împreună 9 ore, lucrarea a fost terminată de numai una din echipe în 7 ore și 30 minute. În cât timp ar finaliza lucrarea fiecare echipă lucrând singură?
Soluție:

Noțiunea de viteză se poate extinde și la alte mărimi, de exemplu de natură economică, financiară.
Problema 5: Un cont bancar, cu soldul inițial de 2020 de lei este alimentat zilnic cu suma de 20 de lei / zi și tot zilnic din el se plătește o dobândă de 1 % din suma existentă la începutul zilei respective.
- Cât este soldul după cea de-a 12-a zi?
- Care este viteza zilnică de variație a contului (balanța zilnică)?
Soluție:

Concluzie
Problemele rezolvate, chiar dacă nu conțin în enunț mărimi specifice celor de mișcare (viteză, distanță parcursă…), implică un anumit “ritm” al acțiunii și factorul „timp”, ceea ce le permite o astfel de abordare.
Din perspectiva didacticii matematicii, abordarea prezentată în acest articol oferă un exemplu remarcabil de generalizare a unui model matematic și de aplicare a acestuia în rezolvarea unor probleme din categorii diverse. Valoarea pedagogică a acestei metode rezidă în capacitatea sa de a evidenția structura matematică comună a unor situații problematice aparent neînrudite, dezvoltând astfel la elevi competența de a identifica schemele algoritmice transferabile. Prin utilizarea modelului vitezei ca raport între o mărime și timpul necesar, se cultivă gândirea relațională și se consolidează înțelegerea profundă a conceptului de proporționalitate inversă, element fundamental în matematica gimnazială. Această abordare didactică transcende simpla tehnică de rezolvare, reprezentând un exercițiu de gândire matematică avansată care promovează flexibilitatea cognitivă, abstractizarea și capacitatea de a construi modele matematice. Implementarea acestei metode în practica educațională contribuie la formarea unei viziuni coerente asupra matematicii ca știință a modelelor și relațiilor, pregătind elevii pentru abordări complexe în studiul ulterior al domeniilor STEM, unde identificarea izomorfismelor structurale între fenomene diverse constituie o competență esențială.
Bibliografie
1. Colecția revistei “Gazeta Matematică”;
2. Troacă Victor, “Bazele contabilității“, Editura Sitech, Craiova, 2012.

Trebuie să fii autentificat pentru a publica un comentariu.