Se știe că, în matematică, de multe ori anumite rezultate se intuiesc, dar pentru a putea fi considerate adevăruri și pentru a putea constitui, la rândul lor, puncte de plecare pentru alte descoperiri, ele trebuie demonstrate. Demonstrația, succesiunea logică de idei ce decurg unele dintr-altele, este apanajul oricărui rezultat matematic. Înainte de a aplica o formulă, de a folosi un enunț, noi trebuie să știm sigur în ce condiții sau pentru ce valori este el adevărat.
Una dintre afirmațiile despre care s-a bănuit a fi adevărată, dar care s-a lăsat foarte greu dovedită, se numește Marea Teoremă a lui Fermat și povestea ei este atât de fascinantă, încât poate trezi interesul tuturor, mai mult sau mai puțin pasionați de matematică.
Are, spre mulțumirea noastră, are un enunț ce poate fi înțeles ușor:

Teorema poartă numele francezului Pierre de Fermat (1601-1665), de profesie jurist, care a fost membru al Parlamentului din Toulouse în perioada în care Cardinalul Richelieu era prim-ministru al Franței – o epocă plină de intrigi și comploturi. Numai că Fermat n-a fost interesat de problemele politice ale vremii, pentru că avea o altă mare pasiune – matematica, și tot timpul liber și-l dedica studiului în acest domeniu. S-a dovedit un matematician autodidact genial, pionier în domeniile probabilităților și analizei, interesat de o mulțime de lucruri. Studia din Aritmetica lui Diofant, un manual practic ce își propunea să descrie teoria numerelor servindu-se de o serie de probleme și soluțiile lor. Dar nu se mărginea doar la a înțelege problemele, ci și la a crea altele noi pe care încerca să le rezolve, observații și frânturi de demonstrații fiind notate pe spațiile goale dintre textele cărții. În dreptul Problemei nr. 8 a notat:
„Este imposibil ca un cub să fie exprimat ca suma a două cuburi sau ca puterea a patra să fie rescrisă ca suma a două puteri de ordin patru sau, în general, ca orice număr care este o putere mai mare decât doi să reprezinte o sumă de puteri, ca în cazul pătratului.
Mă aflu în posesia unei demonstrații minunate a aceste afirmații, dar marginea paginii este prea strâmtă pentru a o cuprinde.”
Si astfel, mănușa a fost aruncată. Care să fi fost oare acea demonstrație? Găsirea ei a fost o provocare ce a frământat multe minți și a stârnit multe controverse vreme de 350 de ani.
Se știe că această ecuație, pentru n=2:
![]()
are un număr infinit de soluții, de exemplu
![]()
Recunoaștem aici celebra teoremă demonstrată pentru prima dată de Pitagora (apr. 600 î.Ch.) dar cunoscută cu mult înainte de învățații chinezi și indieni: „În orice triunghi dreptunghic suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei.”
Dar pentru n mai mare decât 2 ecuațiile ce se generau astfel păreau fără soluție.
Primul care a făcut un pas înainte spre demonstrarea celor de mai sus a fost matematicianul elvețian, considerat una din cele mai fantastice minți ale secolului XVIII, Leonard Euler (1707-1783). El a găsit printre notițele lui Fermat indicații de rezolvare pentru ecuația
![]()
a pus la punct această demonstrație și apoi a reușit să rezolve problema și pentru n=3 (x^3+y^3=z^3), introducând pentru prima dată în matematică noțiunea de număr imaginar, cel pe care azi îl notăm cu i și care are pătratul egal cu -1. S-a observat că atunci problema este rezolvată și pentru orice n multiplu de 3 sau 4 și că, de fapt, problema se reduce la rezolvarea cazurilor când n este număr prim (număr natural care are exact doi divizori). Dar mulțimea numerelor prime este infinită!
Apoi o franțuzoaică, Sophie Germain (1776-1831), care studia la Ecole Polytechnique deghizată în domnul Le Blanc, întrucât instituția era destinată doar bărbaților, a oferit o metodă ce si-a dovedit pe deplin succesul în 1825 când alți doi talentați matematicieni, Dirichlet și Legendre, au fost capabili, cu ajutorul ei, să demonstreze că ecuația nu are soluții nici pentru n=5.
Paisprezece ani mai târziu, al treilea francez, Lame, aducând completări ingenioase metodei lui Germain, a demonstrat și cazul numărului prim 7.
Academia Franceză de Știință a oferit o serie de premii, inclusiv o medalie de aur și 3000 de franci matematicianului care avea să rezolve o dată pentru totdeauna misterul Marii Teoreme. La întrunirea din 1 martie 1847, mai mulți savanți și-au expus teoriile și au promis demonstrații, dar la un studiu atent acestea s-au dovedit incorecte. Alte memorii s-au depus mai târziu, în 1856, dar cu același rezultat.
Speranțele erau mai firave ca oricând și problema a ajuns într-un con de umbră până în 1908, când Paul Wolfskehl, un industriaș german, a readus lucrurile la viață. Poveste începe cu pasiunea acestui domn pentru o femeie care nu-i împărtășea sentimentele și, nefericit, hotărăște să se sinucidă la prima bătaie a gongului într-un miez de noapte. Eficient fiind, a terminat toate pregătirile mai repede și în timpul rămas s-a delectat cu una din încercările de demonstrație ale Teoremei lui Fermat. Lectura l-a fascinat, n-a auzit gongul și planurile s-au schimbat. La citirea testamentului său în 1908, familia a fost șocată să constate că o mare parte a averii (1 milion de lire) a fost alocată ca premiu celui ce va demonstra primul teorema. A fost recunoscător enigmei care i-a salvat viața. Până în 1970, au fost înregistrate 621 de memorii la departamentul de matematică al Universității din Göttingen, dar fără succes.
Problema ne duce mai departe în Japonia anilor de după Război, unde, în 1955, la un simpozion internațional tinerii Goro Shimura (1930-2019) și Yutaka Taniyama (1927-1958) au adus la cunoștința lumii matematice o observație a lor, și anume că două domenii aparent diferite ale universului matematic, ecuațiile eliptice și formele modulare, funcționează de fapt după aceleași reguli, că fiecărei ecuații eliptice îi corespunde o formă modulară și reciproc. Această afirmație revoluționară, cunoscută sub numele de conjectura Taniyama-Shimura, avea să fie cheia problemei.
O ecuație eliptică are forma
![]()
unde a, b, c sunt numere întregi. Problema lor, ca și în cazul oricărei ecuații, este găsirea soluțiilor, respectiv aici, dacă admit soluții întregi și care sunt acestea. Ecuațiile eliptice se cunoșteau din vremea lui Diofant (apr. 250 d Ch.) însă marea lor diversitate și complexitate le propune și azi ca un obiect de studiu deloc facil.
Formele modulare, pe de altă parte, sunt unele dintre cele mai abstracte entități matematice. Au grade infinite de simetrie, acestea pot fi permutate, comutate, reflectate sau rotite într-o infinitate de moduri și totuși rămân neschimbate.

Principala lor caracteristică este că sunt exprimate prin patru dimensiuni, ale căror coordonate sunt date de numere complexe. Sunt greu de imaginat, pentru că ele sunt exprimate prin patru dimensiuni (spațiu hiperbolic).

Întrebarea rămâne: care este legătura lor cu problema lui Fermat?
În 1984, Gerhard Freay (n. 1944), un matematician din Saarbrücken, a făcut o afirmație la un Simpozion din Germania, pe care a și justificat-o: dacă cineva ar demonstra conjectura Taniyama-Shimura, ar rezolva imediat Marea Teoremă a lui Fermat. Pentru că, dacă presupunem că teorema are soluții, de exemplu numerele notate A,B,C (care verifică deci relația A^n+B^n=C^n ), atunci ecuația x^n+y^n=z^n se poate rearanja, după transformări complicate, în forma
![]()
care este o ecuație eliptică. Dacă se poate demonstra că ea nu are o formă modulară atașată înseamnă că ea nu există, deoarece, conform conjecturii Taniyama-Shimura, orice ecuație eliptică are o formă modulară pereche. Dacă ea nu există, înseamnă că soluțiile A,B,C nu există, deci presupunerea noastră că ecuația x^n+y^n=z^n are soluții este falsă și Marea Teorema a lui Fermat este adevărată.
Ken Ribet (n. 1948), profesor la Universitatea California din Berkeley, a reușit să demonstreze în vara lui 1986, că da, ecuația eliptică propusă de Freay nu are o formă modulară atașată.
A rămas de demonstrat conjectura Taniyama-Shimura și acest lucru a fost reușit de către matematicianul englez Andrew Wiles (n. 1953). Profesor atunci la Harvard, a considerat că este o șansă pe care viața i-o oferă, să încerce rezolvarea unei probleme care-l fascina încă din copilărie. A decis să lucreze în completă izolare și taină. A preluat de la colegi tehnici moderne de investigație pe care le-a perfectat și rafinat și, cu pași mici și cu o hotărâre și încredere demne de invidie, a fost gata să anunțe după 7 ani marele eveniment, conjectura era demonstrată. La Conferința din iunie 1993, Institutul Isaac Newton din Cambridge, Andrew Wiles era considerat un erou. Ziarele lumii au cedat primele pagini pentru relatarea acestui fapt.
Dar nimic nu este certificat în matematică fără o verificare oficială, Comitetul Wolfskehl așteptând și el verificarea manuscrisului și publicarea lui pentru acordarea premiului. Puțini matematicieni ai lumii pot fi referenți ai unui asemenea material, șase dintre ei au împărțit documentul și au început studiul. Atunci când s-a găsit o eroare în Capitolul 3, castelul părea că se prăbușise. Zvonurile că de fapt și această demonstrație era falsă străbăteau planeta, însă Andrew Wiles spera că eroarea este remediabilă. Supliciul a durat un an. Dăruit cu inspirație pentru extraordinara sa perseverență, Andrew anunță în 1994 soluția finală. În mai 1995, această capodoperă a matematicii moderne este publicată în Annals of Mathematics.
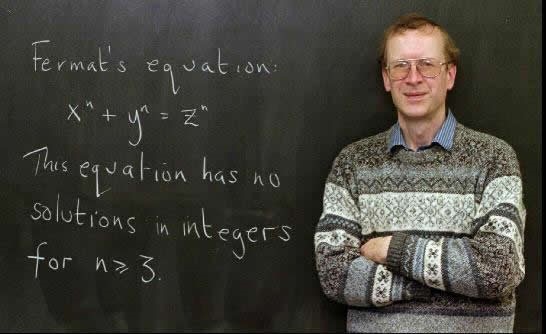
Bibliografie
Singh, Simon, Marea Teoremă a lui Fermat, Editura Humanitas, 2012
Stewart, Ian, Îmblânzirea infinitului, Povestea Matematicii, Editura Humanitas, 2011
scientia.ro/stiinta-la-minut/48-scurta-istorie-descoperiri-stiintifice/839-marea-teorema-a-lui-fermat-matematica-la-superlativ-2.html
golem.ph.utexas.edu/category/2008/02/modular_forms.html
